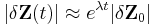Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, engineering, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the butterfly effect. Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for chaotic systems, rendering long-term prediction impossible in general.[1] This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved.[2] In other words, the deterministic nature of these systems does not make them predictable.[3][4] This behavior is known as deterministic chaos, or simply chaos.
Chaotic behavior can be observed in many natural systems, such as the weather.[5] Explanation of such behavior may be sought through analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincaré maps.
Contents[hide] |
Applications
Chaos theory is applied in many scientific disciplines: geology, mathematics, programming, microbiology, biology, computer science, economics,[6][7][8] engineering,[9] finance,[10][11] meteorology, philosophy, physics, politics, population dynamics, psychology, and robotics.
Chaotic behavior has been observed in the laboratory in a variety of systems including electrical circuits, lasers, oscillating chemical reactions, fluid dynamics, and mechanical and magneto-mechanical devices, as well as computer models of chaotic processes. Observations of chaotic behavior in nature include changes in weather,[5] the dynamics of satellites in the solar system, the time evolution of the magnetic field of celestial bodies, population growth in ecology, the dynamics of the action potentials in neurons, and molecular vibrations. There is some controversy over the existence of chaotic dynamics in plate tectonics and in economics.[12][13][14]
A successful application of chaos theory is in ecology where dynamical systems such as the Ricker model have been used to show how population growth under density dependence can lead to chaotic dynamics.
Chaos theory is also currently being applied to medical studies of epilepsy, specifically to the prediction of seemingly random seizures by observing initial conditions.[15]
Quantum chaos theory studies how the correspondence between quantum mechanics and classical mechanics works in the context of chaotic systems.[16] Recently, another field, called relativistic chaos,[17] has emerged to describe systems that follow the laws of general relativity.
The motion of N stars in response to their self-gravity (the gravitational N-body problem) is generically chaotic.[18]
In electrical engineering, chaotic systems are used in communications, random number generators, and encryption systems.
In numerical analysis, the Newton-Raphson method of approximating the roots of a function can lead to chaotic iterations if the function has no real roots.[19]
Chaotic dynamics
In common usage, "chaos" means "a state of disorder".[20] However, in chaos theory, the term is defined more precisely. Although there is no universally accepted mathematical definition of chaos, a commonly used definition says that, for a dynamical system to be classified as chaotic, it must have the following properties:[21]
- it must be sensitive to initial conditions;
- it must be topologically mixing; and
- its periodic orbits must be dense.
The requirement for sensitive dependence on initial conditions implies that there is a set of initial conditions of positive measure which do not converge to a cycle of any length.
Sensitivity to initial conditions
Sensitivity to initial conditions means that each point in such a system is arbitrarily closely approximated by other points with significantly different future trajectories. Thus, an arbitrarily small perturbation of the current trajectory may lead to significantly different future behaviour. However, it has been shown that the last two properties in the list above actually imply sensitivity to initial conditions[22][23] and if attention is restricted to intervals, the second property implies the other two[24] (an alternative, and in general weaker, definition of chaos uses only the first two properties in the above list[25]). It is interesting that the most practically significant condition, that of sensitivity to initial conditions, is actually redundant in the definition, being implied by two (or for intervals, one) purely topological conditions, which are therefore of greater interest to mathematicians.
Sensitivity to initial conditions is popularly known as the "butterfly effect", so called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science in Washington, D.C. entitled Predictability: Does the Flap of a Butterfly’s Wings in Brazil set off a Tornado in Texas? The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different.
A consequence of sensitivity to initial conditions is that if we start with only a finite amount of information about the system (as is usually the case in practice), then beyond a certain time the system will no longer be predictable. This is most familiar in the case of weather, which is generally predictable only about a week ahead.[26]
The Lyapunov exponent characterises the extent of the sensitivity to initial conditions. Quantitatively, two trajectories in phase space with initial separation 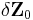 diverge
diverge
where λ is the Lyapunov exponent. The rate of separation can be different for different orientations of the initial separation vector. Thus, there is a whole spectrum of Lyapunov exponents — the number of them is equal to the number of dimensions of the phase space. It is common to just refer to the largest one, i.e. to the Maximal Lyapunov exponent (MLE), because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.
There are also measure-theoretic mathematical conditions (discussed in ergodic theory) such as mixing or being a K-system which relate to sensitivity of initial conditions and chaos.[4]
Topological mixing
Topological mixing (or topological transitivity) means that the system will evolve over time so that any given region or open set of its phase space will eventually overlap with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.
Topological mixing is often omitted from popular accounts of chaos, which equate chaos with sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points will eventually become widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behaviour: all points except 0 tend to infinity.
Density of periodic orbits
Density of periodic orbits means that every point in the space is approached arbitrarily closely by periodic orbits. Topologically mixing systems failing this condition may not display sensitivity to initial conditions, and hence may not be chaotic. For example, an irrational rotation of the circle is topologically transitive, but does not have dense periodic orbits, and hence does not have sensitive dependence on initial conditions.[27] The one-dimensional logistic map defined by x → 4 x (1 – x) is one of the simplest systems with density of periodic orbits. For example, 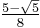 →
→ 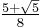 →
→ 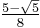 (or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).[28]
(or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).[28]
Sharkovskii's theorem is the basis of the Li and Yorke[29] (1975) proof that any one-dimensional system which exhibits a regular cycle of period three will also display regular cycles of every other length as well as completely chaotic orbits.
Strange attractors
Some dynamical systems, like the one-dimensional logistic map defined by x → 4 x (1 – x), are chaotic everywhere, but in many cases chaotic behaviour is found only in a subset of phase space. The cases of most interest arise when the chaotic behaviour takes place on an attractor, since then a large set of initial conditions will lead to orbits that converge to this chaotic region.
An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it was not only one of the first, but it is also one of the most complex and as such gives rise to a very interesting pattern which looks like the wings of a butterfly.
Unlike fixed-point attractors and limit cycles, the attractors which arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set which forms at the boundary between basins of attraction of fixed points – Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and a fractal dimension can be calculated for them.
Minimum complexity of a chaotic system
Discrete chaotic systems, such as the logistic map, can exhibit strange attractors whatever their dimensionality. However, the Poincaré-Bendixson theorem shows that a strange attractor can only arise in a continuous dynamical system (specified by differential equations) if it has three or more dimensions. Finite dimensional linear systems are never chaotic; for a dynamical system to display chaotic behaviour it has to be either nonlinear, or infinite-dimensional.
The Poincaré–Bendixson theorem states that a two dimensional differential equation has very regular behavior. The Lorenz attractor discussed above is generated by a system of three differential equations with a total of seven terms on the right hand side, five of which are linear terms and two of which are quadratic (and therefore nonlinear). Another well-known chaotic attractor is generated by the Rossler equations with seven terms on the right hand side, only one of which is (quadratic) nonlinear. Sprott[30] found a three dimensional system with just five terms on the right hand side, and with just one quadratic nonlinearity, which exhibits chaos for certain parameter values. Zhang and Heidel[31][32] showed that, at least for dissipative and conservative quadratic systems, three dimensional quadratic systems with only three or four terms on the right hand side cannot exhibit chaotic behavior. The reason is, simply put, that solutions to such systems are asymptotic to a two dimensional surface and therefore solutions are well behaved.
While the Poincaré–Bendixson theorem means that a continuous dynamical system on the Euclidean plane cannot be chaotic, two-dimensional continuous systems with non-Euclidean geometry can exhibit chaotic behaviour. Perhaps surprisingly, chaos may occur also in linear systems, provided they are infinite-dimensional.[33] A theory of linear chaos is being developed in the functional analysis, a branch of mathematical analysis.
History
An early proponent of chaos theory was Henri Poincaré. In the 1880s, while studying the three-body problem, he found that there can be orbits which are nonperiodic, and yet not forever increasing nor approaching a fixed point.[34][35] In 1898 Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature.[36] In the system studied, "Hadamard's billiards", Hadamard was able to show that all trajectories are unstable in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent.
Much of the earlier theory was developed almost entirely by mathematicians, under the name of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out by G.D. Birkhoff,[37] A. N. Kolmogorov,[38][39][40] M.L. Cartwright and J.E. Littlewood,[41] and Stephen Smale.[42] Except for Smale, these studies were all directly inspired by physics: the three-body problem in the case of Birkhoff, turbulence and astronomical problems in the case of Kolmogorov, and radio engineering in the case of Cartwright and Littlewood. Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.
Despite initial insights in the first half of the twentieth century, chaos theory became formalized as such only after mid-century, when it first became evident for some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behaviour of certain experiments like that of the logistic map. What had been beforehand excluded as measure imprecision and simple "noise" was considered by chaos theories as a full component of the studied systems.
The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical, while figures and images made it possible to visualize these systems.
An early pioneer of the theory was Edward Lorenz whose interest in chaos came about accidentally through his work on weather prediction in 1961.[43] Lorenz was using a simple digital computer, a Royal McBee LGP-30, to run his weather simulation. He wanted to see a sequence of data again and to save time he started the simulation in the middle of its course. He was able to do this by entering a printout of the data corresponding to conditions in the middle of his simulation which he had calculated last time.
To his surprise the weather that the machine began to predict was completely different from the weather calculated before. Lorenz tracked this down to the computer printout. The computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.506127 was printed as 0.506. This difference is tiny and the consensus at the time would have been that it should have had practically no effect. However Lorenz had discovered that small changes in initial conditions produced large changes in the long-term outcome.[44] Lorenz's discovery, which gave its name to Lorenz attractors, showed that even detailed atmospheric modelling cannot in general make long-term weather predictions. Weather is usually predictable only about a week ahead.[26]
The year before, Benoît Mandelbrot found recurring patterns at every scale in data on cotton prices.[45] Beforehand, he had studied information theory and concluded noise was patterned like a Cantor set: on any scale the proportion of noise-containing periods to error-free periods was a constant – thus errors were inevitable and must be planned for by incorporating redundancy.[46] Mandelbrot described both the "Noah effect" (in which sudden discontinuous changes can occur) and the "Joseph effect" (in which persistence of a value can occur for a while, yet suddenly change afterwards).[47][48] This challenged the idea that changes in price were normally distributed. In 1967, he published "How long is the coast of Britain? Statistical self-similarity and fractional dimension", showing that a coastline's length varies with the scale of the measuring instrument, resembles itself at all scales, and is infinite in length for an infinitesimally small measuring device.[49] Arguing that a ball of twine appears to be a point when viewed from far away (0-dimensional), a ball when viewed from fairly near (3-dimensional), or a curved strand (1-dimensional), he argued that the dimensions of an object are relative to the observer and may be fractional. An object whose irregularity is constant over different scales ("self-similarity") is a fractal (for example, the Koch curve or "snowflake", which is infinitely long yet encloses a finite space and has fractal dimension equal to circa 1.2619, the Menger sponge and the Sierpiński gasket). In 1975 Mandelbrot published The Fractal Geometry of Nature, which became a classic of chaos theory. Biological systems such as the branching of the circulatory and bronchial systems proved to fit a fractal model.
Chaos was observed by a number of experimenters before it was recognized; e.g., in 1927 by van der Pol[50] and in 1958 by R.L. Ives.[51][52] However, as a graduate student in Chihiro Hayashi's laboratory at Kyoto University, Yoshisuke Ueda was experimenting with analog computers (that is, vacuum tubes) and noticed, on Nov. 27, 1961, what he called "randomly transitional phenomena". Yet his advisor did not agree with his conclusions at the time, and did not allow him to report his findings until 1970.[53][54]
In December 1977 the New York Academy of Sciences organized the first symposium on Chaos, attended by David Ruelle, Robert May, James A. Yorke (coiner of the term "chaos" as used in mathematics), Robert Shaw (a physicist, part of the Eudaemons group with J. Doyne Farmer and Norman Packard who tried to find a mathematical method to beat roulette, and then created with them the Dynamical Systems Collective in Santa Cruz, California), and the meteorologist Edward Lorenz.
The following year, Mitchell Feigenbaum published the noted article "Quantitative Universality for a Class of Nonlinear Transformations", where he described logistic maps.[55] Feigenbaum notably discovered the universality in chaos, permitting an application of chaos theory to many different phenomena.
In 1979, Albert J. Libchaber, during a symposium organized in Aspen by Pierre Hohenberg, presented his experimental observation of the bifurcation cascade that leads to chaos and turbulence in Rayleigh–Bénard convection systems. He was awarded the Wolf Prize in Physics in 1986 along with Mitchell J. Feigenbaum "for his brilliant experimental demonstration of the transition to turbulence and chaos in dynamical systems".[56]
Then in 1986 the New York Academy of Sciences co-organized with the National Institute of Mental Health and the Office of Naval Research the first important conference on Chaos in biology and medicine. There, Bernardo Huberman presented a mathematical model of the eye tracking disorder among schizophrenics.[57] This led to a renewal of physiology in the 1980s through the application of chaos theory, for example in the study of pathological cardiac cycles.
In 1987, Per Bak, Chao Tang and Kurt Wiesenfeld published a paper in Physical Review Letters[58] describing for the first time self-organized criticality (SOC), considered to be one of the mechanisms by which complexity arises in nature. Alongside largely lab-based approaches such as the Bak–Tang–Wiesenfeld sandpile, many other investigations have focused on large-scale natural or social systems that are known (or suspected) to display scale-invariant behaviour. Although these approaches were not always welcomed (at least initially) by specialists in the subjects examined, SOC has nevertheless become established as a strong candidate for explaining a number of natural phenomena, including: earthquakes (which, long before SOC was discovered, were known as a source of scale-invariant behaviour such as the Gutenberg–Richter law describing the statistical distribution of earthquake sizes, and the Omori law[59] describing the frequency of aftershocks); solar flares; fluctuations in economic systems such as financial markets (references to SOC are common in econophysics); landscape formation; forest fires; landslides; epidemics; and biological evolution (where SOC has been invoked, for example, as the dynamical mechanism behind the theory of "punctuated equilibria" put forward by Niles Eldredge and Stephen Jay Gould). Given the implications of a scale-free distribution of event sizes, some researchers have suggested that another phenomenon that should be considered an example of SOC is the occurrence of wars. These "applied" investigations of SOC have included both attempts at modelling (either developing new models or adapting existing ones to the specifics of a given natural system), and extensive data analysis to determine the existence and/or characteristics of natural scaling laws.
The same year, James Gleick published Chaos: Making a New Science, which became a best-seller and introduced the general principles of chaos theory as well as its history to the broad public, (though his history under-emphasized important Soviet contributions). At first the domain of work of a few, isolated individuals, chaos theory progressively emerged as a transdisciplinary and institutional discipline, mainly under the name of nonlinear systems analysis. Alluding to Thomas Kuhn's concept of a paradigm shift exposed in The Structure of Scientific Revolutions (1962), many "chaologists" (as some described themselves) claimed that this new theory was an example of such a shift, a thesis upheld by J. Gleick.
The availability of cheaper, more powerful computers broadens the applicability of chaos theory. Currently, chaos theory continues to be a very active area of research, involving many different disciplines (mathematics, topology, physics, population biology, biology, meteorology, astrophysics, information theory, etc.).
Distinguishing random from chaotic data
It can be difficult to tell from data whether a physical or other observed process is random or chaotic, because in practice no time series consists of pure 'signal.' There will always be some form of corrupting noise, even if it is present as round-off or truncation error. Thus any real time series, even if mostly deterministic, will contain some randomness.[60][61]
All methods for distinguishing deterministic and stochastic processes rely on the fact that a deterministic system always evolves in the same way from a given starting point.[60][62] Thus, given a time series to test for determinism, one can:
- pick a test state;
- search the time series for a similar or 'nearby' state; and
- compare their respective time evolutions.
Define the error as the difference between the time evolution of the 'test' state and the time evolution of the nearby state. A deterministic system will have an error that either remains small (stable, regular solution) or increases exponentially with time (chaos). A stochastic system will have a randomly distributed error.[63]
Essentially all measures of determinism taken from time series rely upon finding the closest states to a given 'test' state (e.g., correlation dimension, Lyapunov exponents, etc.). To define the state of a system one typically relies on phase space embedding methods.[64] Typically one chooses an embedding dimension, and investigates the propagation of the error between two nearby states. If the error looks random, one increases the dimension. If you can increase the dimension to obtain a deterministic looking error, then you are done. Though it may sound simple it is not really. One complication is that as the dimension increases the search for a nearby state requires a lot more computation time and a lot of data (the amount of data required increases exponentially with embedding dimension) to find a suitably close candidate. If the embedding dimension (number of measures per state) is chosen too small (less than the 'true' value) deterministic data can appear to be random but in theory there is no problem choosing the dimension too large – the method will work.
When a non-linear deterministic system is attended by external fluctuations, its trajectories present serious and permanent distortions. Furthermore, the noise is amplified due to the inherent non-linearity and reveals totally new dynamical properties. Statistical tests attempting to separate noise from the deterministic skeleton or inversely isolate the deterministic part risk failure. Things become worse when the deterministic component is a non-linear feedback system.[65] In presence of interactions between nonlinear deterministic components and noise, the resulting nonlinear series can display dynamics that traditional tests for nonlinearity are sometimes not able to capture.[66]
The question of how to distinguish deterministic chaotic systems from stochastic systems has also been discussed in philosophy.[67]
Cultural references
Chaos theory has been mentioned in numerous movies and works of literature. For instance, it was mentioned extensively in Michael Chrichton's novel Jurassic Park and more briefly in its sequel. Other examples include the film Chaos, The Butterfly Effect, the sitcom The Big Bang Theory, Tom Stoppard's play Arcadia and the video games Tom Clancy's Splinter Cell: Chaos Theory and Assassin's Creed (video game). The influence of chaos theory in shaping the popular understanding of the world we live in was the subject of the BBC documentary High Anxieties - The Mathematics of Chaos directed by David Malone. Chaos theory is also the subject of discussion in the BBC documentary "The Secret Life of Chaos" presented by the physicist Jim Al-Khalili.
See also
References
- ^ Stephen H. Kellert, In the Wake of Chaos: Unpredictable Order in Dynamical Systems, University of Chicago Press, 1993, p 32, ISBN 0-226-42976-8.
- ^ Kellert, p. 56.
- ^ Kellert, p. 62.
- ^ a b Werndl, Charlotte (2009). What are the New Implications of Chaos for Unpredictability?. The British Journal for the Philosophy of Science 60, 195-220.
- ^ a b Sneyers Raymond (1997). "Climate Chaotic Instability: Statistical Determination and Theoretical Background". Environmetrics 8 (5): 517–532.
- ^ Kyrtsou C., Labys W. (2006). "Evidence for chaotic dependence between US inflation and commodity prices". Journal of Macroeconomics 28 (1): 256–266. doi:10.1016/j.jmacro.2005.10.019.
- ^ Kyrtsou C., Labys W. (2007). "Detecting positive feedback in multivariate time series: the case of metal prices and US inflation". Physica A 377 (1): 227–229. doi:10.1016/j.physa.2006.11.002.
- ^ Kyrtsou, C., and Vorlow, C., (2005). Complex dynamics in macroeconomics: A novel approach, in New Trends in Macroeconomics, Diebolt, C., and Kyrtsou, C., (eds.), Springer Verlag.
- ^ Applying Chaos Theory to Embedded Applications
- ^ Hristu-Varsakelis, D., and Kyrtsou, C., (2008): Evidence for nonlinear asymmetric causality in US inflation, metal and stock returns, Discrete Dynamics in Nature and Society, Volume 2008, Article ID 138547, 7 pages, doi:10.1155/2008/138547.
- ^ Kyrtsou, C. and M. Terraza, (2003). "Is it possible to study chaotic and ARCH behaviour jointly? Application of a noisy Mackey-Glass equation with heteroskedastic errors to the Paris Stock Exchange returns series,". Computational Economics 21 (3): 257–276. doi:10.1023/A:1023939610962.
- ^ Apostolos Serletis and Periklis Gogas,Purchasing Power Parity Nonlinearity and Chaos, in: Applied Financial Economics, 10, 615–622, 2000.
- ^ Apostolos Serletis and Periklis Gogas The North American Gas Markets are ChaoticPDF (918 KB), in: The Energy Journal, 20, 83–103, 1999.
- ^ Apostolos Serletis and Periklis Gogas, Chaos in East European Black Market Exchange Rates, in: Research in Economics, 51, 359–385, 1997.
- ^ Comdig.org, Complexity Digest 199.06
- ^ Michael Berry, "Quantum Chaology," pp 104–5 of Quantum: a guide for the perplexed by Jim Al-Khalili (Weidenfeld and Nicolson 2003)."?". http://www.physics.bristol.ac.uk/people/berry_mv/the_papers/Berry358.pdf.
- ^ A. E. Motter, Relativistic chaos is coordinate invariant, in: Phys. Rev. Lett. 91, 231101 (2003).
- ^ Hemsendorf, M.; Merritt, D. (November 2002). "Instability of the Gravitational N-Body Problem in the Large-N Limit". The Astrophysical Journal 580 (1): 606–609. arXiv:astro-ph/0205538. Bibcode 2002ApJ...580..606H. doi:10.1086/343027
- ^ Strang, Gilbert, "A chaotic search for i," The College Mathematics Journal 22(1), January 1991, 3-12.
- ^ Definition of chaos at Wiktionary;
- ^ Hasselblatt, Boris; Anatole Katok (2003). A First Course in Dynamics: With a Panorama of Recent Developments. Cambridge University Press. ISBN 0521587506.
- ^ Saber N. Elaydi, Discrete Chaos, Chapman & Hall/CRC, 1999, page 117, ISBN 1-58488-002-3.
- ^ William F. Basener, Topology and its applications, Wiley, 2006, page 42, ISBN 0-471-68755-3,
- ^ Michel Vellekoop; Raoul Berglund, "On Intervals, Transitivity = Chaos," The American Mathematical Monthly, Vol. 101, No. 4. (April, 1994), pp. 353–355 [1]
- ^ Alfredo Medio and Marji Lines, Nonlinear Dynamics: A Primer, Cambridge University Press, 2001, page 165, ISBN 0-521-55874-3.
- ^ a b Robert G. Watts, Global Warming and the Future of the Earth, Morgan & Claypool, 2007, page 17.
- ^ Devaney, Robert L. (2003). An Introduction to Chaotic Dynamical Systems, 2nd ed. Westview Press. ISBN 0-8133-4085-3.
- ^ Alligood, K. T., Sauer, T., and Yorke, J.A. (1997). Chaos: an introduction to dynamical systems. Springer-Verlag New York, LLC. ISBN 0-387-94677-2.
- ^ Li, T. Y. and Yorke, J. A. "Period Three Implies Chaos." American Mathematical Monthly 82, 985–92, 1975.[2]
- ^ Sprott, J.C. (1997). "Simplest dissipative chaotic flow". Physics Letters A 228 (4-5): 271. Bibcode 1997PhLA..228..271S. doi:10.1016/S0375-9601(97)00088-1.
- ^ Fu, Z.; Heidel, J. (1997). "Non-chaotic behaviour in three-dimensional quadratic systems". Nonlinearity 10 (5): 1289. Bibcode 1997Nonli..10.1289F. doi:10.1088/0951-7715/10/5/014.
- ^ Heidel, J.; Fu, Z. (1999). "Nonchaotic behaviour in three-dimensional quadratic systems II. The conservative case". Nonlinearity 12 (3): 617. Bibcode 1999Nonli..12..617H. doi:10.1088/0951-7715/12/3/012.
- ^ Bonet, J.; Martínez-Giménez, F.; Peris, A. (2001). "A Banach space which admits no chaotic operator". Bulletin of the London Mathematical Society 33 (2): 196–198. doi:10.1112/blms/33.2.196.
- ^ Jules Henri Poincaré (1890) "Sur le problème des trois corps et les équations de la dynamique. Divergence des séries de M. Lindstedt," Acta Mathematica, vol. 13, pages 1–270.
- ^ Florin Diacu and Philip Holmes (1996) Celestial Encounters: The Origins of Chaos and Stability, Princeton University Press.
- ^ Hadamard, Jacques (1898). "Les surfaces à courbures opposées et leurs lignes géodesiques". Journal de Mathématiques Pures et Appliquées 4: pp. 27–73.
- ^ George D. Birkhoff, Dynamical Systems, vol. 9 of the American Mathematical Society Colloquium Publications (Providence, Rhode Island: American Mathematical Society, 1927)
- ^ Kolmogorov, Andrey Nikolaevich (1941). "Local structure of turbulence in an incompressible fluid for very large Reynolds numbers". Doklady Akademii Nauk SSSR 30 (4): 301–305. Bibcode 1941DoSSR..30..301K. Reprinted in: Proceedings of the Royal Society of London: Mathematical and Physical Sciences (Series A), vol. 434, pages 9–13 (1991).
- ^ Kolmogorov, A. N. (1941). "On degeneration of isotropic turbulence in an incompressible viscous liquid". Doklady Akademii Nauk SSSR 31 (6): 538–540. Reprinted in: Proceedings of the Royal Society of London: Mathematical and Physical Sciences (Series A), vol. 434, pages 15–17 (1991).
- ^ Kolmogorov, A. N. (1954). "Preservation of conditionally periodic movements with small change in the Hamiltonian function". Doklady Akademii Nauk SSSR 98: 527–530. See also Kolmogorov–Arnold–Moser theorem
- ^ Mary L. Cartwright and John E. Littlewood (1945) "On non-linear differential equations of the second order, I: The equation y" + k(1−y2)y' + y = bλkcos(λt + a), k large," Journal of the London Mathematical Society, vol. 20, pages 180–189. See also: Van der Pol oscillator
- ^ Stephen Smale (January 1960) "Morse inequalities for a dynamical system," Bulletin of the American Mathematical Society, vol. 66, pages 43–49.
- ^ Edward N. Lorenz, "Deterministic non-periodic flow," Journal of the Atmospheric Sciences, vol. 20, pages 130–141 (1963).
- ^ Gleick, James (1987). Chaos: Making a New Science. London: Cardinal. p. 17. ISBN 043429554X.
- ^ Mandelbrot, Benoît (1963). "The variation of certain speculative prices". Journal of Business 36: pp. 394–419.
- ^ Berger J.M., Mandelbrot B. (1963). "A new model for error clustering in telephone circuits". I.B.M. Journal of Research and Development 7: 224–236.
- ^ B. Mandelbrot, The Fractal Geometry of Nature (N.Y., N.Y.: Freeman, 1977), page 248.
- ^ See also: Benoît B. Mandelbrot and Richard L. Hudson, The (Mis)behavior of Markets: A Fractal View of Risk, Ruin, and Reward (N.Y., N.Y.: Basic Books, 2004), page 201.
- ^ Benoît Mandelbrot (5 May 1967) "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension," Science, Vol. 156, No. 3775, pages 636–638.
- ^ B. van der Pol and J. van der Mark (1927) "Frequency demultiplication," Nature, vol. 120, pages 363–364. See also: Van der Pol oscillator
- ^ R.L. Ives (10 October 1958) "Neon oscillator rings," Electronics, vol. 31, pages 108–115.
- ^ See p. 83 of Lee W. Casperson, "Gas laser instabilities and their interpretation," pages 83–98 in: N. B. Abraham, F. T. Arecchi, and L. A. Lugiato, eds., Instabilities and Chaos in Quantum Optics II: Proceedings of the NATO Advanced Study Institute, Il Ciocco, Italy, June 28–July 7, 1987 (N.Y., N.Y.: Springer Verlag, 1988).
- ^ Ralph H. Abraham and Yoshisuke Ueda, eds., The Chaos Avant-Garde: Memoirs of the Early Days of Chaos Theory (Singapore: World Scientific Publishing Co., 2001). See Chapters 3 and 4.
- ^ Sprott, J. Chaos and time-series analysis. Oxford. University Press, Oxford, UK, & New York, US. 2003
- ^ Mitchell Feigenbaum (July 1978) "Quantitative universality for a class of nonlinear transformations," Journal of Statistical Physics, vol. 19, no. 1, pages 25–52.
- ^ "The Wolf Prize in Physics in 1986.". http://www.wolffund.org.il/cat.asp?id=25&cat_title=PHYSICS.
- ^ Bernardo Huberman, "A Model for Dysfunctions in Smooth Pursuit Eye Movement" Annals of the New York Academy of Sciences, Vol. 504 Page 260 July 1987, Perspectives in Biological Dynamics and Theoretical Medicine
- ^ Per Bak, Chao Tang, and Kurt Wiesenfeld, "Self-organized criticality: An explanation of the 1/f noise," Physical Review Letters, vol. 59, no. 4, pages 381–384 (27 July 1987). However, the conclusions of this article have been subject to dispute. "?". http://www.nslij-genetics.org/wli/1fnoise/1fnoise_square.html.. See especially: Lasse Laurson, Mikko J. Alava, and Stefano Zapperi, "Letter: Power spectra of self-organized critical sand piles," Journal of Statistical Mechanics: Theory and Experiment, 0511, L001 (15 September 2005).
- ^ F. Omori (1894) "On the aftershocks of earthquakes," Journal of the College of Science, Imperial University of Tokyo, vol. 7, pages 111–200.
- ^ a b Provenzale A. et al.: "Distinguishing between low-dimensional dynamics and randomness in measured time-series", in: Physica D, 58:31–49, 1992
- ^ Brock, W. A., "Distinguishing random and deterministic systems: Abridged version," Journal of Economic Theory 40, October 1986, 168-195.
- ^ Sugihara G., May R. (1990). "Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series" (PDF). Nature 344 (6268): 734–741. doi:10.1038/344734a0. PMID 2330029. http://deepeco.ucsd.edu/~george/publications/90_nonlinear_forecasting.pdf.
- ^ Casdagli, Martin. "Chaos and Deterministic versus Stochastic Non-linear Modelling", in: Journal Royal Statistics Society: Series B, 54, nr. 2 (1991), 303-28
- ^ Broomhead D. S. and King G. P.: "Extracting Qualitative Dynamics from Experimental Data", in: Physica 20D, 217–36, 1986
- ^ Kyrtsou C (2008). "Re-examining the sources of heteroskedasticity: the paradigm of noisy chaotic models". Physica A 387 (27): 6785–6789. doi:10.1016/j.physa.2008.09.008.
- ^ Kyrtsou, C., (2005). Evidence for neglected linearity in noisy chaotic models, International Journal of Bifurcation and Chaos, 15(10), pp. 3391–3394.
- ^ Werndl, Charlotte (2009c). Are Deterministic Descriptions and Indeterministic Descriptions Observationally Equivalent?. Studies in History and Philosophy of Modern Physics 40, 232-242.
Scientific literature
Articles
- A.N. Sharkovskii, "Co-existence of cycles of a continuous mapping of the line into itself", Ukrainian Math. J., 16:61–71 (1964)
- Li, T. Y. and Yorke, J. A. "Period Three Implies Chaos." American Mathematical Monthly 82, 985–92, 1975.
- Crutchfield, J.P., Farmer, J.D., Packard, N.H., & Shaw, R.S (December 1986). "Chaos". Scientific American 255 (6): 38–49 (bibliography p.136). Bibcode 1986SciAm.255...38T Online version (Note: the volume and page citation cited for the online text differ from that cited here. The citation here is from a photocopy, which is consistent with other citations found online, but which don't provide article views. The online content is identical to the hardcopy text. Citation variations will be related to country of publication).
- Kolyada, S. F. "Li-Yorke sensitivity and other concepts of chaos", Ukrainian Math. J. 56 (2004), 1242–1257.
- C. Strelioff, A. Hübler (2006). Medium-Term Prediction of Chaos, PRL 96, 044101
- A. Hübler, G. Foster, K. Phelps (2007). Managing Chaos: Thinking out of the Box Complexity, vol. 12, pp. 10–13
Textbooks
- Alligood, K. T., Sauer, T., and Yorke, J.A. (1997). Chaos: an introduction to dynamical systems. Springer-Verlag New York, LLC. ISBN 0-387-94677-2.
- Baker, G. L. (1996). Chaos, Scattering and Statistical Mechanics. Cambridge University Press. ISBN 0-521-39511-9.
- Badii, R.; Politi A. (1997). Complexity: hierarchical structures and scaling in physics. Cambridge University Press. ISBN 0521663857. http://www.cambridge.org/catalogue/catalogue.asp?isbn=0521663857.
- Collet, Pierre, and Eckmann, Jean-Pierre (1980). Iterated Maps on the Interval as Dynamical Systems. Birkhauser. ISBN 0-8176-4926-3.
- Devaney, Robert L. (2003). An Introduction to Chaotic Dynamical Systems, 2nd ed,. Westview Press. ISBN 0-8133-4085-3.
- Gollub, J. P.; Baker, G. L. (1996). Chaotic dynamics. Cambridge University Press. ISBN 0-521-47685-2.
- Guckenheimer, J., and Holmes P. (1983). Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer-Verlag New York, LLC. ISBN 0-387-90819-6.
- Gutzwiller, Martin (1990). Chaos in Classical and Quantum Mechanics. Springer-Verlag New York, LLC. ISBN 0-387-97173-4.
- Hoover, William Graham (1999,2001). Time Reversibility, Computer Simulation, and Chaos. World Scientific. ISBN 981-02-4073-2.
- Kautz, Richard (2011). Chaos: The Science of Predictable Random Motion. Oxford University Press. ISBN 978-0-19-959458-0.
- Kiel, L. Douglas; Elliott, Euel W. (1997). Chaos Theory in the Social Sciences. Perseus Publishing. ISBN 0-472-08472-0.
- Moon, Francis (1990). Chaotic and Fractal Dynamics. Springer-Verlag New York, LLC. ISBN 0-471-54571-6.
- Ott, Edward (2002). Chaos in Dynamical Systems. Cambridge University Press New, York. ISBN 0-521-01084-5.
- Strogatz, Steven (2000). Nonlinear Dynamics and Chaos. Perseus Publishing. ISBN 0-7382-0453-6.
- Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850840-9.
- Tél, Tamás; Gruiz, Márton (2006). Chaotic dynamics: An introduction based on classical mechanics. Cambridge University Press. ISBN 0-521-83912-2.
- Tufillaro, Abbott, Reilly (1992). An experimental approach to nonlinear dynamics and chaos. Addison-Wesley New York. ISBN 0-201-55441-0.
- Zaslavsky, George M. (2005). Hamiltonian Chaos and Fractional Dynamics. Oxford University Press. ISBN 0-198-52604-0.
Semitechnical and popular works
- Ralph H. Abraham and Yoshisuke Ueda (Ed.), The Chaos Avant-Garde: Memoirs of the Early Days of Chaos Theory, World Scientific Publishing Company, 2001, 232 pp.
- Michael Barnsley, Fractals Everywhere, Academic Press 1988, 394 pp.
- Richard J Bird, Chaos and Life: Complexity and Order in Evolution and Thought, Columbia University Press 2003, 352 pp.
- John Briggs and David Peat, Turbulent Mirror: : An Illustrated Guide to Chaos Theory and the Science of Wholeness, Harper Perennial 1990, 224 pp.
- John Briggs and David Peat, Seven Life Lessons of Chaos: Spiritual Wisdom from the Science of Change, Harper Perennial 2000, 224 pp.
- Lawrence A. Cunningham, From Random Walks to Chaotic Crashes: The Linear Genealogy of the Efficient Capital Market Hypothesis, George Washington Law Review, Vol. 62, 1994, 546 pp.
- Predrag Cvitanović, Universality in Chaos, Adam Hilger 1989, 648 pp.
- Leon Glass and Michael C. Mackey, From Clocks to Chaos: The Rhythms of Life, Princeton University Press 1988, 272 pp.
- James Gleick, Chaos: Making a New Science, New York: Penguin, 1988. 368 pp.
- John Gribbin, Deep Simplicity,
- L Douglas Kiel, Euel W Elliott (ed.), Chaos Theory in the Social Sciences: Foundations and Applications, University of Michigan Press, 1997, 360 pp.
- Arvind Kumar, Chaos, Fractals and Self-Organisation; New Perspectives on Complexity in Nature , National Book Trust, 2003.
- Hans Lauwerier, Fractals, Princeton University Press, 1991.
- Edward Lorenz, The Essence of Chaos, University of Washington Press, 1996.
- Chapter 5 of Alan Marshall (2002) The Unity of nature, Imperial College Press: London
- Heinz-Otto Peitgen and Dietmar Saupe (Eds.), The Science of Fractal Images, Springer 1988, 312 pp.
- Clifford A. Pickover, Computers, Pattern, Chaos, and Beauty: Graphics from an Unseen World , St Martins Pr 1991.
- Ilya Prigogine and Isabelle Stengers, Order Out of Chaos, Bantam 1984.
- Heinz-Otto Peitgen and P. H. Richter, The Beauty of Fractals : Images of Complex Dynamical Systems, Springer 1986, 211 pp.
- David Ruelle, Chance and Chaos, Princeton University Press 1993.
- Ivars Peterson, Newton's Clock: Chaos in the Solar System, Freeman, 1993.
- David Ruelle, Chaotic Evolution and Strange Attractors, Cambridge University Press, 1989.
- Peter Smith, Explaining Chaos, Cambridge University Press, 1998.
- Ian Stewart, Does God Play Dice?: The Mathematics of Chaos , Blackwell Publishers, 1990.
- Steven Strogatz, Sync: The emerging science of spontaneous order, Hyperion, 2003.
- Yoshisuke Ueda, The Road To Chaos, Aerial Pr, 1993.
- M. Mitchell Waldrop, Complexity : The Emerging Science at the Edge of Order and Chaos, Simon & Schuster, 1992.
External links
- Nonlinear Dynamics Research Group with Animations in Flash
- The Chaos group at the University of Maryland
- The Chaos Hypertextbook. An introductory primer on chaos and fractals
- ChaosBook.org An advanced graduate textbook on chaos (no fractals)
- Society for Chaos Theory in Psychology & Life Sciences
- Nonlinear Dynamics Research Group at CSDC, Florence Italy
- Interactive live chaotic pendulum experiment, allows users to interact and sample data from a real working damped driven chaotic pendulum
- Nonlinear dynamics: how science comprehends chaos, talk presented by Sunny Auyang, 1998.
- Nonlinear Dynamics. Models of bifurcation and chaos by Elmer G. Wiens
- Gleick's Chaos (excerpt)
- Systems Analysis, Modelling and Prediction Group at the University of Oxford
- A page about the Mackey-Glass equation
- High Anxieties - The Mathematics of Chaos (2008) BBC documentary directed by David Malone
|
||||||||||||||